数据结构

前言

数据结构的复习，涵盖往日学习的树、图、查询、排序算法
日后补充链表等顺序表、队列操作🖊

树

深度：节点层次

度：节点的子树数

叶子：度为0的节点

分支结点

子结点

父结点

兄弟结点：有同一个父结点的结点

无序树：左右无序

有序树：左右有序

森林：多个不相交的树的集合

二叉树

二叉树是个有序树，每个结点至多有两棵子树

性质

1. 在二叉树上的第 i 层上至多有 $2^{i-1}$个结点

2. 深度为k的二叉树至多有 $2^k-1$个结点

3. 对任何一棵二叉树T，如果其叶子数为 $n_0$，度为2的结点数为$n_2$，则有 $n_0=n_2+1$

   证明3：

   1. 二叉树内所有结点数为 $n=n_0+n_1+n_2$
   2. 二叉树内总分支数都由度为1和2的结点射出，总结点数为 $n_1+2n_2$
   3. 总分支树代表子结点数，再加上根节点（唯一的非子结点）得：$n=n_1+2n_2+1$
   4. 结合1，3得 $n_0=n_2+1$

4. 满二叉树：深度为 k 且结点数为$2^k-1$的二叉树（满了）

   完全二叉树

   1. 具有 n 个结点的完全二叉树的深度为 $[log_2n]+1$
   2. $i=1$ 的结点为根节点，$i>1$ 的结点的父节点为 $[i/2]$
   3. 如果 $2i>n$ ，则结点 i 是叶子结点，否则其左孩子为 $2i$
   4. 如果 $2i>n$ ，则结点 i 无右孩子，否则其右孩子为 $2i+1$

二叉树的存储结构

数组（计算得出结点）

根据性质计算出结点位置

链式存储（模拟了逻辑模型）

每个结点存储一个左孩子，右孩子和数据，还可以存储父节点

树的存储结构

双亲表示法

孩子表示法

孩子兄弟表示法（二叉树表示法）

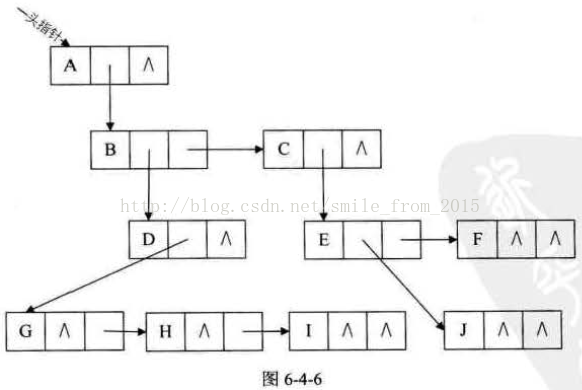
遍历二叉树

先序遍历

1. 根节点
2. 左子树
3. 右子树

中序遍历

1. 左子树
2. 根结点
3. 右子树

后序遍历

1. 左子树
2. 右子树
3. 根节点

根据先序遍历和中序遍历还原二叉树或后序遍历

算法1

输入：前序遍历，中序遍历
1、寻找树的root，前序遍历的第一节点G就是root。
2、观察前序遍历GDAFEMHZ，知道了G是root，剩下的节点必然在root的左或右子树中的节点。
3、观察中序遍历ADEFGHMZ。其中root节点G左侧的ADEF必然是root的左子树中的节点，G右侧的HMZ必然是root的右子树中的节点，root不在中序遍历的末尾或开始就说明根节点的两颗子树都不为空。
4、观察左子树ADEF，按照前序遍历的顺序来排序为DAFE，因此左子树的根节点为D，并且A是左子树的左子树中的节点，EF是左子树的右子树中的节点。
5、同样的道理，观察右子树节点HMZ，前序为MHZ，因此右子树的根节点为M，左子节点H，右子节点Z。

观察发现，上面的过程是递归的。先找到当前树的根节点，然后划分为左子树，右子树，然后进入左子树重复上面的过程，然后进入右子树重复上面的过程。最后就可以还原一棵树了：

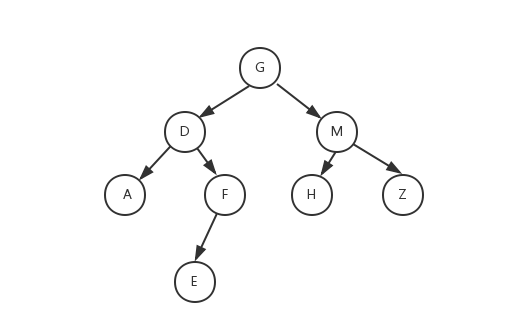
从而得到PostOrder: AEFDHZMG

改进：
更进一步说，其实，如果仅仅要求写后续遍历，甚至不要专门占用空间保存还原后的树。只需要用一个数组保存将要得到的后序，就能实现：

算法2

输入：一个保存后序的数组，前序遍历，中序遍历
1、确定根,放在数组末尾
2、确定左子树的索引范围，放在数组中相同索引的位置。
3、确定右子树索引范围，放在数组中对应索引的位置，刚好能放下。
4、用左子树的前序遍历和中序遍历，把后序遍历保存在对应索引的位置
5、用左子树的前序遍历和中序遍历，把后序遍历保存在对应索引的位置

哈夫曼树（最优二叉树）

路径长度

带权路径长度

哈夫曼树：所有叶子结点的带权路径长度之和最小

构造哈夫曼树

数等价

二叉树与一般树转换

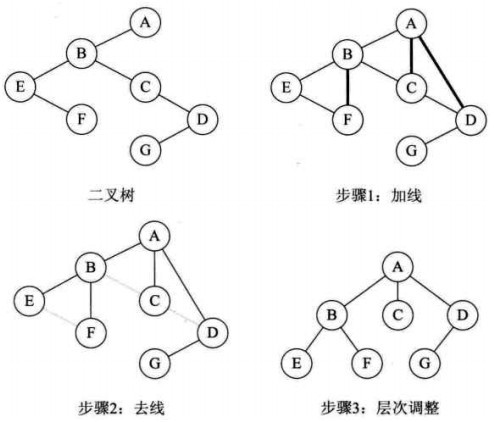
一般树转二叉树

1. 将每一个结点与他的兄弟结点之间连一条线。

2. 对每一个双亲结点，只保留它与第一个子结点的连线，删除与其余结点的连线。

3. 整理，左右摆齐。

二叉树转一般树（反过程）

1. 若一个结点是其父结点的左结点，则将此结点的右结点，右结点的右结点……都与其父结点相连线。

2. 删除原二叉树所有父结点与右结点的连线。

3. 整理连线，统一高度。

图

顶点

有向图

• 弧
  • 弧头/初始点
  • 弧尾/终结点

无向图

• 边

$$G=(V,\{A\})$$

设n为顶点数目，e为边或弧的数目

无向图中 $0\leq$ $e\leq\frac{1}{2}n(n-1)$

完全图：$e=\frac{1}{2}n(n-1)$的无向图

有向完全图：$e=n(n-1)$的有向图

稀疏图：边或弧很少的图

稠密图

子图：有两个图$G=(V,\{E\})$和$G'=(V',\{E'\})$，若$V'\subseteq V$且$E'\subseteq E$，则 G‘ 是 G 的子图

邻接点：对于无向图$G=(V,\{E\})$，有边$(v,v’)\in E$，则称顶点 v 和 v’ 互为邻接点；边$(v,v’)$与顶点 v 和 v’ 相关联。

度$TD(v)$(degree)：顶点关联的边的数目

入度$ID(v)$(indegree)：

出度$OD(v)$(outdegree)：

图的度数之和等于边的两倍：$e=\frac{1}{2}\sum^n_{i=1}TD(v_i)$

路径：

回路/环：第一个顶点和最后一个顶点相同的路径

简单路径：顶点不重复出现的路径

连通：无向图中，顶点间有路径，则称为连通

连通图：图中任意点都是连通的，就是连通图

连通分量：非连通图中的极大连通子图

强连通图：有向图中所有顶点都存在路径

强连通分量：有向图中的极大强连通子图

生成树：一个连通图的极小连通子图。有连通图中的全部顶点，但只有足以构成一棵树的n-1条边。如果在生成树上增加一条边，必定构成一个环。

生成森林：

图的存储结构

数组表示法：

顶点向量+邻接矩阵

• 邻接矩阵：表示序号为0-n的元素之间的邻接关系（两点间是否有弧）

$$\left[ \begin{matrix} 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 \end{matrix} \right]$$

• 网的邻接矩阵（带权）：

$$\left[ \begin{matrix} ∞ & 5 & 7 & ∞ \\ ∞ & ∞ & ∞ & 1 \\ 12 & 4 & ∞ & ∞ \\ ∞ & 2 & 1 & ∞ \end{matrix} \right]$$

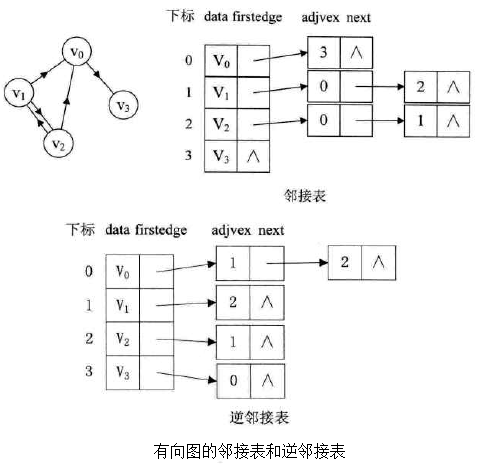
邻接表

图的一种链式存储结构，反映的是节点的出度邻接情况。

逆邻接表

反映的是节点的入度邻接情况

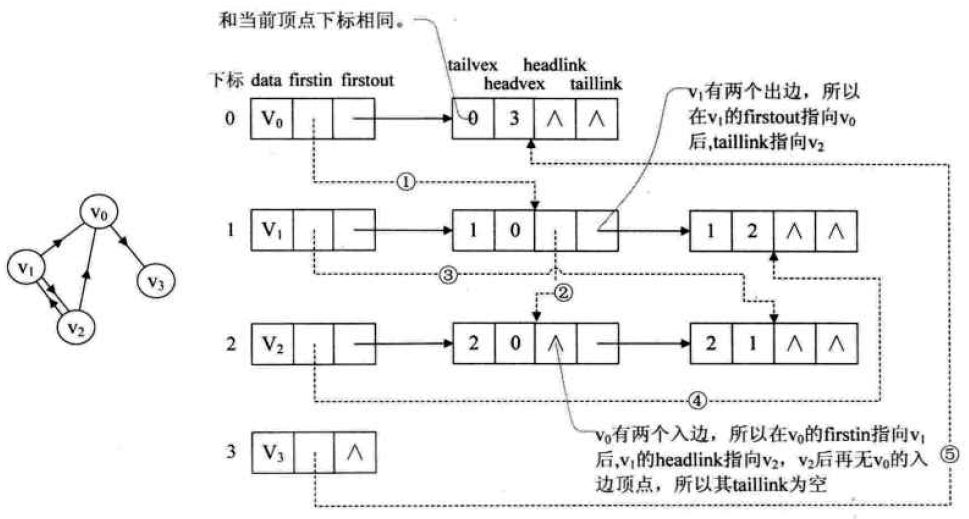
十字链表

有向图的一种优化存储结构。

十字链表的好处就是因为把邻接表和逆邻接表整合在了一起，这样既容易找到以vi为尾的弧，也容易找到以vi为头的弧，因而容易求得顶点的出度和入度。除了结构复杂一点外，其创建图的时间复杂度和邻接表是相同的，因此在某些有向图的应用中，是很有用的工具。

顶点结点

data	firstin	firstout
顶点信息	以该顶点为弧头的第一个弧	以该顶点为弧尾的第一个弧

弧结点

tailvex	headvex	hlink	tlink	info
弧尾位置	弧头位置	弧头相同的下一个弧	弧尾相同的下一个弧	以该顶点为弧尾的第一个弧

邻接多重表

无向图的一种链式存储结构

边：
| mark | ivex | ilink | jvex | jlink | info |
| ———— | —— | ———————————- | —— | ———————————- | ——— |
| 搜索标记 | 顶点 | 下一条依附于 i 顶点的边 | 顶点 | 下一条依附与 j 顶点的边 | 边信息 |

顶点：

data	firstedge
	第一条依附于该顶点的边

图的遍历

深度优先搜索

类似树的先序遍历，先序遍历未被搜索的顶点

如：下面的顺序是$v_1→v_2→v_4→v_8→v_5→v_3→v_6→v_7$

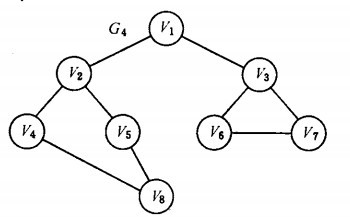
广度优先搜索

类似树的按层次遍历，从v出发依次访问未被访问过的v的邻接点

如：上面的广度优先搜索顺序是：$v_1→v_2→v_3→v_4→v_5→v_6→v_7→v_8$

图的连通性问题

最小生成树

最小代价生成树（权值之和最小）

Prim算法

适用于求边稠密的网的最小生成树

Kruskal算法

适用于求边稀疏的网的最小生成树

最短路径问题

Dijkstra算法

查找

二分查找

O(logn)

静态查找表

动态查找表

二叉排序树

左子树上的所有结点小于根节点的值，右子树所有节点大于根节点，左右子树也是二叉排序树

中序遍历有序，适用于二分查找

平衡二叉树（AVL树）

左子树和右子树的深度之差绝对值不超过1

B-树

B+树

哈希表

处理冲突：

开放地址法

再哈希法

链地址法

建立公共溢出区

排序

插入排序

直接插入排序

复杂度：$O(n^2)$

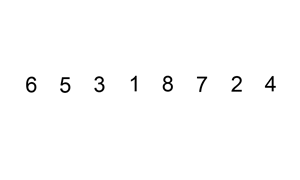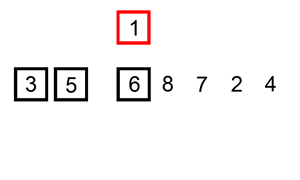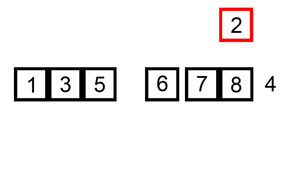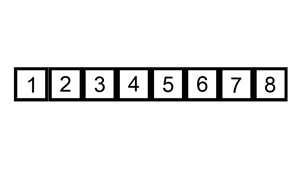
public static void sort(int[] arr){
    int pos,temp;
    for(int i=1;i<arr.length;i++){	// 顺序搜寻
        pos = i;					// 定位坐标
        while(pos!=0&&arr[pos]<arr[pos-1]){		// 逆序交换，直到无法交换为止
            temp = arr[pos];
            arr[pos] = arr[pos-1];
            arr[pos-1] = temp;
            pos--;	// 逆序坐标
        }
    }
}

希尔排序

（缩小增量排序）

简单的希尔排序是减半的增量序列：但是因为增量序列不互质，导致了效率降低（前面白做了几次排序，必须到增量为1的时候做一趟原始的增量排序）

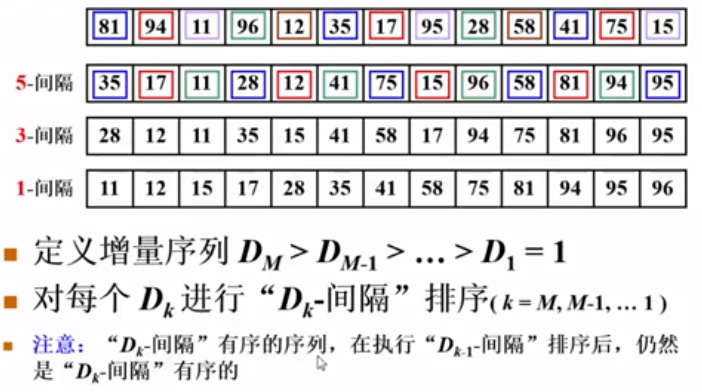
function shellSort(arr) {
    var len = arr.length,
        temp,
        gap = 1;
    while(gap < len/3) {          //动态定义间隔序列
        gap = gap*3+1;
    }
    for (gap; gap > 0; gap = Math.floor(gap/3)) {	// 缩小增量
        for (var i = gap; i < len; i++) {	// 增量范围内的插入排序
            temp = arr[i];
            for (var j = i-gap; j >= 0 && arr[j] > temp; j -= gap) { // 增量范围内的交换
                arr[j+gap] = arr[j];
            }
            arr[j+gap] = temp;
        }
    }
    return arr;
}

冒泡排序

快速排序

选择排序

堆排序